This is part two of series on work in progress with Patrick Allen, Ana Caraiani, Toby Gee, David Helm, Bao Le Hung, James Newton, Peter Scholze, Richard Taylor, and Jack Thorne. Click here for Part I

It has been almost 25 years since Wiles first announced his proof of Taniyama-Shimura, and, truthfully, variations on his method have been pretty much the only game in town since then (this paper included). In all generalizations of this argument, one needs to have some purchase on the integral structure of the automorphic forms involved, which requires that they contribute in some way to the cohomology of an arithmetic manifold (locally symmetric space). This is because it is crucial to be able to exploit the integral structure to study congruences between modular forms. Let’s briefly recall Wiles’ strategy. One starts out with a residual representation

\(\overline{\rho}: G_S \rightarrow \mathrm{GL}_2(\mathbf{F}_p)\)

which one assumes to be modular, that is, is the mod-p reduction of a representation associated to a modular form which is assumed to have some local properties similar to rho. One then considers a deformation ring R which captures all deformations of the residual representation which “look modular” of the right weight and level (some aspects of Serre’s conjecture due to Ribet are empoyed here, although Skinner-Wiles came up with a base change trick to circumvent some of these difficulties). On the automorphic side, one looks at the cohomology groups M = H^1(X,Z_p)_m of modular curves (X = X_0(N)) localized at a maximal ideal m of the Hecke algebra T associated to rhobar, and proves that there is a surjective map:

\(R \rightarrow \mathbf{T}_{\mathfrak{m}}.\)

Already many deep theorems have been used to arrive at this point. To begin, one needs Galois representations associated to modular forms, but moreover, one needs to know that these representations satisfy all of the expected local-global compatibilities at the primes in S. In the case of modular forms, all of these facts were basically known before Wiles.

The next step, which lies at the heart of the Taylor-Wiles method, is to introduce certain auxiliary sets Q of carefully chosen primes, and consider the spaces M_Q = H^1(X_1(Q),Z_p)_m which relate to spaces of modular forms of larger level. If T_Q is the associated Hecke algebra, and R_Q is the corresponding deformation ring in which ramification is allowed not only at S but now also at Q, there are compatible maps as follows:

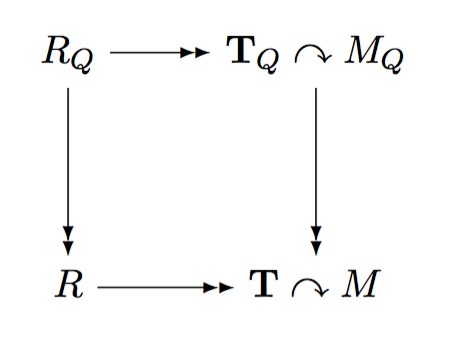
The key point concerning how one chooses the sets Q is to ensure that, even though R_Q may get bigger, its infinitesimal tangent space does not. Hence all the R_Q are quotients of some fixed ring R_oo = Z_p[[X_1,…,X_q]]. (Here q is chosen so that q = |Q|.) In this process, all the rings also have an auxiliary action of a ring S_oo = Z_p[[T_1,…,T_q]] of diamond operators, coming from the Galois group of X_1(Q) over X_0(Q) on the automorphic side, and the inertia groups at Q on the Galois side. The action of S_oo on these modules factors through R_Q by construction, by local global compatibility at primes dividing Q. After throwing away the Galois representations almost entirely (but keeping the diamond operators), one can patch the modules M_Q/p^n for different sets of primes Q, and arrive at a patched module M_oo for R_oo and S_oo such that:

• The module \(M_{\infty}\) has positive rank as an \(S_{\infty}\) module.
• If \(\mathfrak{a}\) is the augmentation ideal of \(S_{\infty},\) then \(R_{\infty}/\mathfrak{a} = R,\) and \(M_{\infty}/\mathfrak{a} = M.\)

The first statement may be viewed as saying that there are “lots” of automorphic forms. On the other hand, the fact that R_oo has the same dimension of S_oo says that there are not “too many” Galois representations. Indeed, this friction is enough in this context to prove that M_oo is free over R_oo, and then to deduce the same claim for M over R, from which R = T follows. (Already included here is a innovation due to Diamond where one deduces freeness as a consequence rather than building it in as an assumption.) The argument I have very briefly sketched above is really only a proof of modularity in the minimal case. The general case requires a completely separate argument to bootstrap from minimal to non-minimal level using two further ingredients: Wiles’ numerical criterion, and a lower bound on the congruence ideal necessary to apply the numerical criterion, which ultimately follows from Ihara’s Lemma.

The “first generation” of improvements to Wiles consisted of understanding enough integral p-adic Hodge theory to make the required arugments on the Galois side. Notable papers here include the work of Conrad-Diamond-Taylor and Breuil-Conrad-Diamond-Taylor (but let us also not forget here the contribution of The Hawk). Improvements along these lines continue to today, and are very closely interwined with p-adic Langlands program and work of Breuil, Colmez, Kisin, Emerton, Paškūnas, and many others.

The “second generation” of improvements consisted of relaxing the assumption that R_oo is smooth, by allowing instead R_oo to have multiple components (but still of the same dimension) associated to different components in the local deformation rings at primes in S (at p and away from p). This innovation was due to Kisin, who also introduced the notion of framing to handle this.

The “third generation” of improvements (somewhat orthogonal to the second) cames from replacing 2-dimensional representations with n-dimensional representations, but still under some very restrictive assumptions on the image of rho. One key consequence of these assumptions is that the spaces of modular forms M_Q = H^*(X_1(Q),Z_p)_m all occur inside a single cohomology group, which allows one to control the growth of these spaces when patching. Here one thinks of the work of Clozel-Harris-Taylor. Also pertinent is that the analog of Ihara’s Lemma is open for higher rank groups; Taylor came up with a technique to bypass it when proving modularity lifting theorems now known as “Ihara avoidance.”

(Of course there were many other developments less directly relevant to this post, including but not limited to Skinner-Wiles and Khare-Wintenberger.)

The problem with considering general representations for GL(n) for n > 2, even over Q, is that the automorphic forms are spread over a number of different cohomology groups, in fact in some range [q_0,q_0 + 1, … ,q_0 + l_0] for specific invariants q_0 and l_0.
This manifests itself in two ways:

1. There are not enough automorphic forms; the patched modules M_oo will not be free over S_oo.
2. There are not enough Galois representations: the ring R_oo does not have the same dimension as S_oo but rather dim R_oo = dim S_oo – l_0.

Of course these problems are related! My work with David Geraghty was precisely about showing how to make these problems cancel each other out. The rough idea is as follows. The cohomology groups H^*(X_1(Q),Z_p)_m which contain interesting classes in characteristic zero occur in the range [q_0,…,q_0+l_0]. Suppose one knows this to be true integrally as well, even with coefficients over F_p instead of Z_p. Then instead of patching the cohomology groups M_Q themselves, one instead patches complexes P_Q of length l_0. The result is a complex P_oo of finite free S_oo modules of length l_0, with an action of R_oo on the cohomology of this complex. But the only way the cohomology of this complex can be small enough to admit an action of R_oo is if the complex is a free resolution of the patched module M_oo of cohomology groups in the extreme final degree, and moreover it also implies that M_oo is big enough as in Wiles’ original argument to give an R=T theorem. Note that it is crucial here that one work with the torsion in integral cohomology. It is quite possible that, at all auxiliary levels Q, there are no more automorphic forms at level Q than are were at level 1. (This can only happen for l_0 > 0, and the idea that torsion should be a suitable replacement is the moral of my paper with Barry Mazur.) These argument is also compatible with the improvements to the method including Taylor’s “Ihara Avoidance” argument.

On the other hand, there is a big problem. This argument required many inputs which were completely unknown at the time we worked this out, so our results were very conditional. To be precise, our results were conditional on the following desiderata:

1. The existence of Galois representations on Hecke rings T which acted as endomorphisms of H^*(X,Z/p^nZ) for locally symmetric spaces X associated to GL(n)/F.
2. The stronger claim that the Galois representations constructed in part 1 satisfied the correct “local-global” compatibility statements for all v in S (including v dividing p).
3. The vanishing of the cohomology groups H^i(X,Z/p^nZ)_m outside the range i in [q_0,…,q_0+l_0], for a non-Eisenstein ideal m.

A different approach to some of these questions (which Matt and I discussed, see here) involves first passing to completed cohomology, where one expects (or hopes!) that all the cohomology groups except in degree q_0 should vanish after localization at a non-maximal ideal.

The first big breakthrough was the result of Scholze, who proved part 1 above, at least up to issues concerning a nilpotent ideal (this was discussed previously on this blog). Another innovation appeared in Khare-Thorne, where it was observed that one can sometimes drop the third assumption under the strong condition that there existed global automorphic forms with the exact level structure corresponding to the original representation. (Unfortunately, in the l_0 > 0 setting, there is no way to produce such forms.)

So this is roughly where we stood in 2016. The key new ingredient which led to this project was the new result of Caraiani and Scholze proving vanishing theorems for the cohomology of non-compact Shimura varieties in degrees above the middle dimension (localized at m) under the assumption of certain genericity hypotheses on m. Since the cohomology of the boundary (for suitably chosen Shimura varieties) is precisely related to the cohomology of arithmetic locally symmetric spaces for GL(n) over CM fields, this allowed for the first time a new construction of the Galois representations for GL(n) which directly related them to the Galois representations coming from geometry. (I say “directly related,” but perhaps I mean simply more direct than Peter’s original construction.) In particular, it was clear to Caraiani and Scholze that this result should have implications for the required local-global compatibility result above. Meanwhile, the IAS had just started a new series of workshops on emerging topics. I guess that Richard must have had conversations with Ana about her work with Peter, which led them to choosing this as the theme, namely:

Ana Caraiani and Peter Scholze are hopeful of extending the methods of their joint paper arXiv:1511.02418 to non-compact Shimura varieties. This would give a new way to attack local-global compatibility at p for some of the Galois representations Scholze attached to torsion classes in the cohomology of arithmetic locally symmetric spaces. The aim of this workshop will be to understand how much local-global compatibility can be proved and to explore the consequences of this, particularly for modularity questions.

So now (1) was available, there was an approach to (2), and a technique for avoiding (3). One issue with the Khare-Thorne trick, however, was that it involved localizing at some prime ideal of characteristic zero, and so did not interact so well with Ihara Avoidance, which was crucial for any sort of applicable theorem. Here’s the subtely, which can be described even in the case when l_0 = 0. The usual Ihara avoidance game is to compare deformation rings R and R’ at Steinberg level and ramified principal series level respectively (after making a base change to ensure that the prime v at the relevant prime q satisfies N(v) = 1 mod p). Let M and M’ be the corresponding modules. One has that M/p = M’/p and R/p = R’/p. Suppose, however, that M behaved perfectly as expected, so that M_oo was free (even of rank one say) over S_oo and free over R_oo. What could happen, if one doesn’t have vanishing of cohomology outside a single degree, is that M’_oo/p = M_oo/p is free over S_oo/p, but that M’_oo is the cohomology of a non-trivial complex S_oo —> S_oo given by multiplication by p. So M’_oo is trivial in characteristic zero, even though M’_oo/p = M_oo/p. So this is a problem. But it is exactly a problem which was resolved during the workshop. The point, very loosely speaking, is that even though the complexes “S_oo” and “S_oo –>[p]—> S_oo” have the same H^0 after reducing modulo p and taking cohomology, their intersection with S_oo/p are quite different on the derived level, so if one can formulate a version of derived Ihara avoidance, then one is in good shape.

So what remained? First, there were a number of technical issues, some of which could be dealt with individually, and one had to make sure that all the fixes were compatible. For example, it is straightforward to modify the original strategy in my paper with David to handle the issue of only having Galois representations up to nilpotence ideals of fixed nilpotence, but one had to make sure this would not interfere with the more subtle derived Ihara avoidance type arguments. Relevant here was the work of Newton and Thorne which placed some of the arguments with complexes more naturally in the derived category. Second, there was the issue of really proving local-global compatibility from the new results of Caraiani-Scholze. A particularly interesting case here was the ordinary case. The rough problem one has to deal with here is deducing that rho is ordinary from knowing that \(\rho \oplus \rho^{\vee}\) is ordinary. But be careful — the latter representation is reducible and so really a pseudo-representation — so it’s not even clear what ordinary this means (though see work of Wake and Wang Erickson, as well as of my student Joel Specter). It turns out that some interesting and subtle things turn up in this case which were found by the “team” of people who wrote up this section. (Although we acheived quite a lot in a week, there were obviously a list of details to be worked out, and we divided ourselves up into certain groups to work on each part of the paper.) But I think we were fairly confident at this point that everything would work out. What was my role in the writing up process you ask? I was selected as the ENFORCER, who goes around harassing everybody else to work and write up their sections of the paper while sipping on Champagne. Presumably I was less selected for my organizational skills and more for my ablity to tell Richard Taylor what to do.

So there we have it! It was clear even during the workshop that some improvements to our arguments were possible, but since the paper is already going to be quite long, we did not try to be completely comprehensive. I expect a number of improvements will follow shortly. I would not be surprised to see in a few years a modularity result for regular weight compatible systems over CM fields which are as complete as the ones (say) in BLGGT.

Finally, I should mention that while the paper is almost completely written, the usual caveats apply about work in progress which has not been completely written up (although we are almost done…)