Last week I was in Cambridge for Barry’s 80th birthday conference. If you are wondering why it took so long for Barry to get a birthday conference, that’s probably because you didn’t know that there was *also* a 60th birthday conference (in 1998, which is not entirely obvious given Barry’s actual birthday). It dates me somewhat to remark that I arrived at Berkeley as a graduate student just in time to miss this conference. (Come July 1, or thereabouts, I will have spent 20 years living in the US.) My first memory of Barry dates from when I was a graduate student in Berkeley. Ken introduced us; we chatted in the tea room (1015), and, as I remember, Barry listened and talked to me with much more generosity and patience than anything I had to say particularly warranted. My next interactions came about through my work with Kevin Buzzard on various conjectures relating to the Eigencurve. Once again, the level of enthusiasm he expressed for our ideas was the type of positive feedback that (to put it mildly) comes somewhat infrequently in academia. He agreed to be my NSF sponsor at Harvard, and later we became co-authors and friends. Needless to say, I was psyched about coming to this conference, and the conference was great! I will not rehash the talks here, beyond a few small observations.
Jordan was very careful about notation in his talk. He had previously used \(X\) as a symbol to denote an integer, so he carefully used \(S\) to denote an object which admits a map to \(B\mathbf{Z}\):
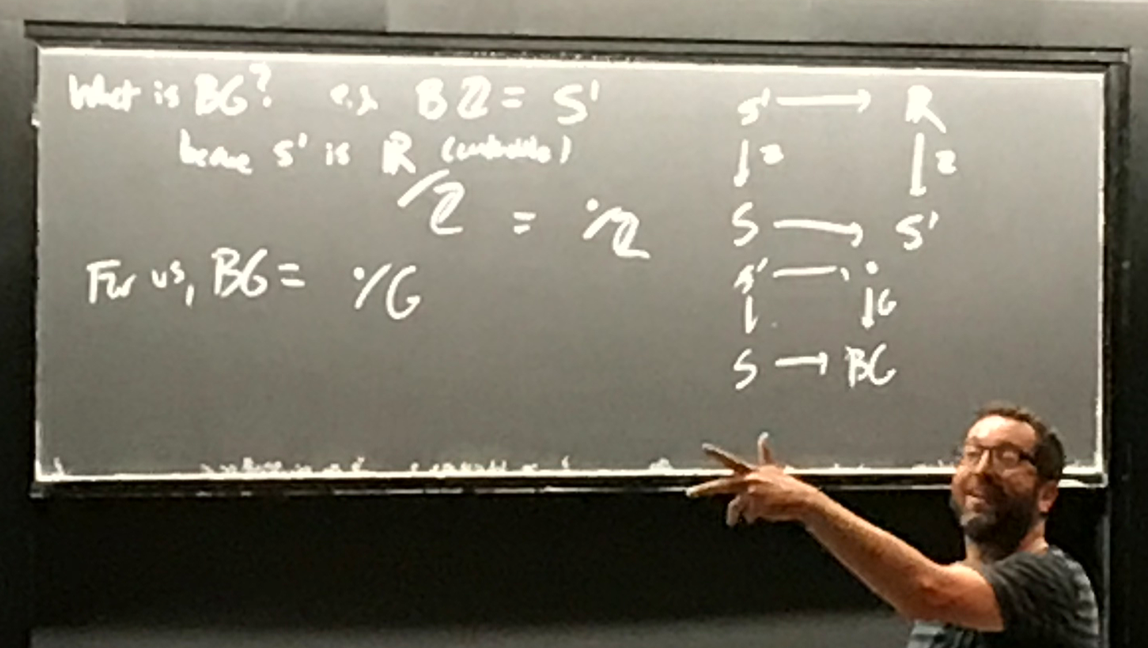
Answered here: What is BG? Not answered here: why do two corners of this pullback square look suspiciously like the same symbol?
As for my own talk, having previously tried to give some technical talks on math related to the CG-method which went horribly wrong, this time I gave a slide talk on my work with Boxer, Gee, and Pilloni which was all candy and no vegetables. (Summary of talk: first Riemann, then Wiles, and now us). Kai-Wen legitimately expressed disappointment at the lack of details (fair enough, you can’t fault that guy for skipping details). Otherwise, it elicited the reminder from Dick Gross that — although I could get by and make a living doing this sort of thing — it was time for number theorists to escape the “ghetto of holomorphic forms” (a phrase I think he attributed to someone else, I should say). Hey, Dick, don’t I at least get points from escaping the even worse “swamplands of discrete series”?
For those playing Barry Mazur bingo (sample squares: Gorenstein, “but…that’s beautiful”, \(X_0(11))\) there were plenty of opportunities to see the influence of Barry’s mathematics. There was, however, a novel aspect of the conference which was an interdisciplinary day consisting of three conversation sessions of Literature/Poetry, History of Science, and Philosophy/Law/Physics respectively. By all accounts this was a wildly successful enterprise (hat-tip to the organizers). I did have one question I would have liked to ask one of the historians of mathematics, but the theme of the conversation meandered elsewhere. Instead I shall ask it here into the void (I’m not accusing you, dear reader, of being a void, merely that there are probably not any actual historians reading this blog):
A working mathematician usually has a very interpretative (and somewhat anachronistic) view of the history of mathematics: Galois “knew” which groups \(\mathrm{PSL}_2(\mathbf{F}_p)\) acted on p points, Gauss “knew” XYZ about class groups, etc. Mathematicians feel confident in these interpretations even if they are not explicitly written in this form in the original texts. What are the dangers in this (Whiggish?) view of the history of mathematics?
Cambridge Culinary Roundup:
With conference banquets (with some touching and amusing speeches by those who knew Barry well) and receptions going on, there was only a limited time for dining, not to mention the problem of trying to book restaurants at the last moment. Still, there was some opportunity to revisit some familiar and some new places:
Burger versus Burger: When it comes to Cambridge burgers, there is only one possible choice…or is there? My general impression was that the only way you could like Mr Bartley’s was if you were first exposed to it before your culinary tastes had a chance to develop (i.e. as a drunk undergraduate). On the other hand, a Cragie on Main burger (circa 2012) was as close in my mind to burger perfection as you could get. But did either of these opinions hold up today? Thus was the origin of the burger versus burger challenge. The participants for round one (Tuesday lunch) included myself, Quomodocumque,
The Hawk, Akshay, Joel, and Bisi. (Although Bisi was participating in a slightly different show, namely the latest episode of “mathematicians trick Bisi into going to a grungy restaurant.”) Round two was Tuesday dinner. Bisi and Joel dropped out on the reasonable basis that they had already consumed enough saturated fat for one week, but the rest of us continued on.
The conclusion? Cragie on Main clearly serves the superior burger (as noted by the Hawk, the fact that the request for a “medium rare” burger came out medium rare at Cragie on Main versus medium well at Bartley’s meant there could be no other conclusion). But perhaps inevitably, my opinions were forced to be somewhat softened in both directions. Bartley’s really did a decent job as far as the overall taste was concerned, and Cragie on Main’s burger — while better — stopped well short of being transformative. I suspect that they’ve been coasting for too long and haven’t maintained the level of excellence they started with (maybe that’s true of Bartley’s too, although I didn’t get a chance to eat there in 1960). In fact, there’s a generally sound principle to be a little wary about restaurants which have been around for too long. (Having said that, I would still find it hard to skip going to Rivoli restaurant on my next trip to Berkeley.)
Chess: Au Bon Pain has disappeared! The entire Holyoke center building is under some sort of reconstruction. The chess players are still around, however, having moved to (literally) the triangle that is Harvard square. I played a few games, and was prettily solidly crushed by a 2300 player in some lightning games. I also declined to play a $10 lightning game against an IM with generous odds, not because I thought I didn’t have a 50% chance of winning, but because I didn’t think I had a 90% chance of winning, and losing would have been at least 10 times more annoying than winning would have been pleasant.
Coffee: 5 (or so) years ago, Crema was a revolution in Harvard Square (i.e. drinkable coffee, reasonable hipster attitude). While their coffee was never at the level of something like Voltage Coffee (near MIT, and sadly now gone), it made staying at the car park known as the Harvard Square Hotel a more palatable option than at the “quaint” Irving street B&B. Times have changed! Crema is a victim of its own success — in a busy place which requires a frequent changeover of staff, the emphasis on coffee no longer seems to be paramount, and the quality control has dropped precipitously. The result was high inconsistency. Out of four coffees I got there, two were OK, one was pretty bad, and one was send directly into the bin. (I would like to have said “tossed in an elegant arc directly into the rubbish bin,” but if I had really attempted that, it would have been more like “unceremoniously spilt all over my shirt.”) As of today, there are definitely better options even in Harvard Square (further afield, one trip was made to Broadsheet which showed promise, even though my own flat white there was merely acceptable). Namely: Tatte Bakery & Cafe, which I really quite liked as far as the pastries and the sandwiches went, and the coffee itself rose to acceptable if not excellent standards.
Darwin’s is still Darwin’s (I prefer Tatte), Night Market (inspired by asian street food) was pretty interesting (some tasty eggplant) if a little idiosyncratic, and Parsnip did a perfectly good job of replacing “Upstairs at the Square,” a restaurant at which I had many a dinner when I used to live in Cambridge. (I had my eye on a few other restaurants, but none of them could take at short notice a reservation for 4 on a Thursday, so Parsnip was especially good given the constraint of not being so popular.
If you have suggestions of better coffee that I may have missed, please make suggestions since I will be returning in November. I also hope the Cambridge weather in November is more like June weather, given that the weather this week was more like November weather:


The “ghetto” quote is related to something André Weil said (in the comments to his collected works, I believe), but I don’t remember it exactly and I don’t have the books handy to check…
I remember well the Mazur 60 conference, since it was the first after my PhD, and it’s the first place I virtually met Jordan (i.e., we both are on the conference picture, but we only really met two months later when we were both postdocs in the same place).
I had trouble finding you at first (http://www.mozzochi.org/Mazur/NEG15.jpg), but I think that’s you next to Tate.
Yes, just behind (it took me a long time to find Tate on the picture…) I note that Jordan is about as far from me as possible….
I found the time today to look up the Weil quote: it’s in the comments in volume 3 of his collected works, precisely those pertaining to his short book (ref. 1976a) “Elliptic functions according to Kronecker and Eisenstein” (“il a fallu Maass pour nous sortir du ghetto des fonctions holomorphes” / “it took Maass to get us out of the ghetto of holomorphic functions”).
Yes, that’s it! (Dick Gross had conveyed it to me faithfully, I had just forgotten the precise wording by the time I wrote this post).
I have no idea what BG is, but that is a great action shot of Jordan!
Well, there’s at least a historian-wannabe reading the blog. Yes, historians worry about (and often dislike) the way mathematicians read older texts. The “what’s really going on here” move that is essential to understanding mathematics can obscure what was really going on historically. (By the way, I find it curious that mathematicians sometimes use the qualifier “morally” to talk about things like this.)
A famous example is Diophantus. One can certainly say that the problems Diophantus solves are mostly finding points on curves of genus 0 or 1, and that the methods he uses are essentially (morally?) the ones we use today: pencils of lines for genus 0 curves, chord-and-tangent for genus 1. And some historians (Bashmakova, Rashed) do just that. Most historians of ancient mathematics would argue that doing so only obscures the historical question of what Diophantus was doing, since there is no chance whatsoever that he was thinking in those terms.
One could argue that the problem because more difficult with more recent texts, particularly ones that have been influential. Since our mathematics is based on them, they sound like modern mathematics. But they may not quite mean what we think they mean. My go-to example is when Descartes says that some roots of polynomials are imaginary.
The “what’s really going on here” move that is essential to understanding mathematics can obscure what was really going on historically.
OK, so let me try to cleave the question along two parallel tracks (mathematical and historical/philosophical). The first is whether “over-interpretation” is dangerous even on a mathematical level. Let me completely make up an ahistorical example. Suppose that we were too quick to interpret Gauss’ work on indefinite quadratic forms in the context of the group structure of class groups of real quadratic fields and say to ourselves “Gauss morally thought of the class group in this way.” But perhaps in reality, Gauss thought about these structures in a genuinely different way, and had we read the texts more faithfully, we would have been quicker to discover the notion of infrastructure (https://www.ams.org/notices/201401/rnoti-p36.pdf) or even Arakelov class groups (https://arxiv.org/pdf/0801.3835.pdf). Could this happen? Does this happen?
Secondly, there is the question of accurate history, whatever that means. I guess mathematicians are motivated in part by wanting to understand the work of the past. But how should I think of what Diophantus was doing? Here one begins to slip towards problems concerning epistemic beliefs. What would it really mean if I said “Diophantus understood parametrizing genus zero curves via pencils of lines”? For example, does it mean the following: having taught Diophantus modern mathematics, when one arrives at the point of explaining the parametrization of genus zero curves, he would recognize it as something he knew. Does it mean more than that?
Let me address the second question, which is easier. I think that most mathematicians who say such things do mean something like what you suggest: “if Diophantus were here and we taught him modern mathematics, he would realize that this is what his method amounted to.” Whether this is true is, of course, beyond our ability to say, which is why it is not helpful as history. What we can do when we want to do history is to attempt to interpret his writings in the light of what we think he (and his contemporaries) knew.
In the case of Diophantus, he pretty much tells us his method: in modern terms we would say that he sets one of his unknowns equal to some expression in the other unknown chosen so that something cancels out. That description, while modern, seems to translate well into Diophantus’s terms. (Recall that he actually had a kind of symbolic notation for polynomials in one variable, so the idea of producing a cancellation would make sense.)
So perhaps the way to say this is that translating into modern terms is the only way we can understand ancient mathematics, but the translation may or may not respect the context, methods, and worldview of the ancient mathematicians. That doesn’t matter for the mathematician seeking (say) inspiration, but it does matter to a historian.
I hope someday I have the privilege to see you literally chuck an unacceptable coffee into the garbage at distance, and I hope I get as good a photo of it as you did of my bad notation!
An actual (somewhat tangential) math question about your talk: when it comes (going back to the original problem) of extensions with Galois group G, there is (as you well know) a natural cover $latex \mathbf{A}^n/G \rightarrow \cdot/G,$ and the source has a nice smooth unirational open subscheme which is much less stacky object and could possibly still be used to count G-extensions (or rather, to count G-polynomials). How does this picture interact (if at all) with your talk or the Malle conjecture more generally?
I had a similar question that I didn’t get around to asking. There is, for example, a “generic polynomial” for cyclic cubic extensions: a one-parameter family of polynomials so that any $C_3$ extension is isomorphic to the splitting field of the polynomial obtained by setting the parameter equal to some value. Typically, however, that value of the parameter is not unique. I’d love to know what the stacky interpretation of this is.
Great question. I answered it with a blog post! https://quomodocumque.wordpress.com/2018/06/26/heights-on-stacks-and-heights-on-vector-bundles-over-stacks/
Pingback: Heights on stacks and heights on vector bundles over stacks | Quomodocumque
That’s an answer to Frank’s question, that is. I’m not sure I know the answer to Fernando’s question!
Pingback: Day 24: Arlington to Boston – LGA to BOS on Foot
Pingback: En Passant VI | Persiflage